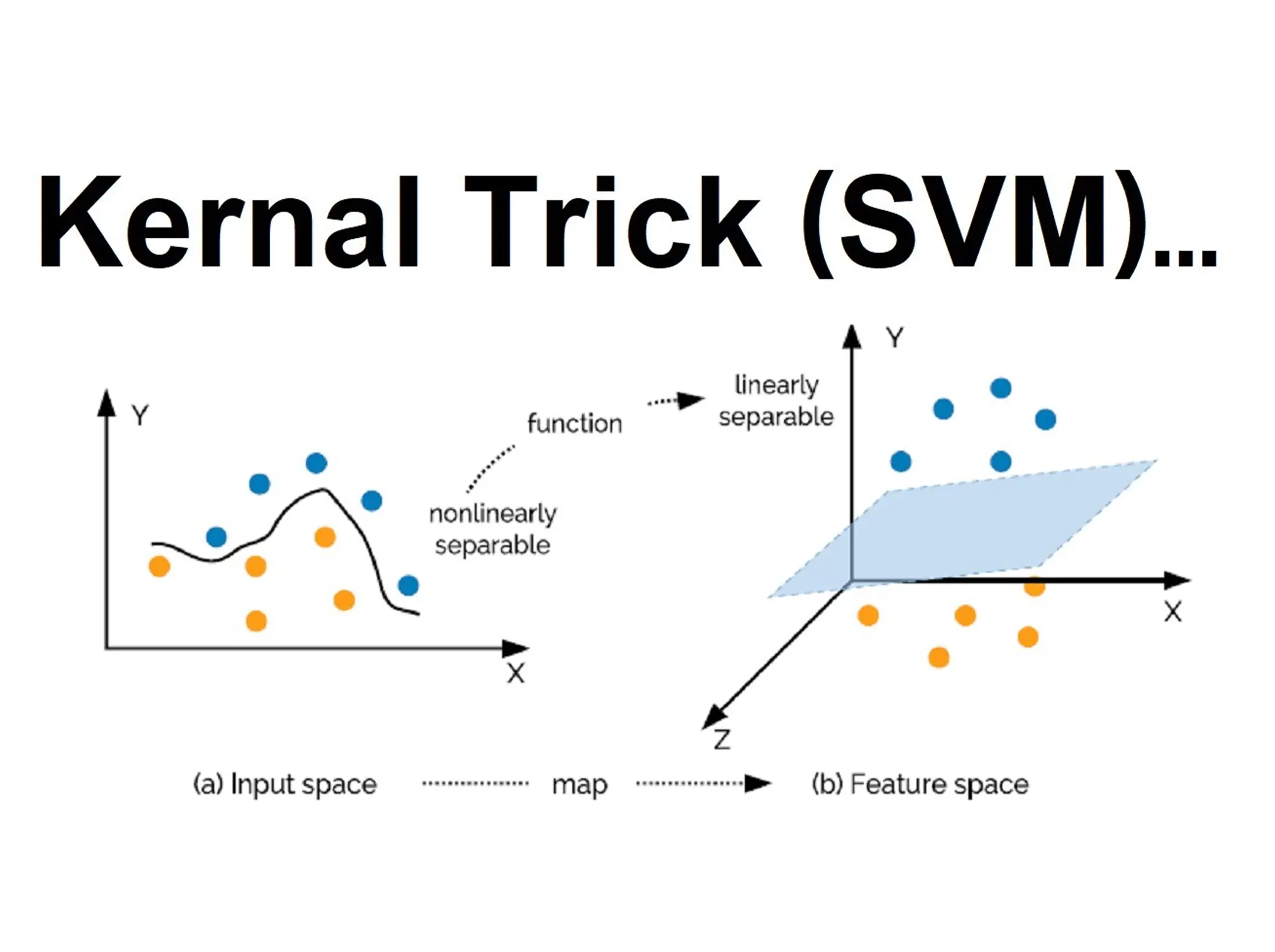
📚📚 Do you know why it is called Kernel “Trick” in SVM.
You must be knowing that the “kernel” or “Kernel function” or “Kernel trick” is a method that allows Support Vector Machines (SVMs) to efficiently operate in high-dimensional feature spaces without explicitly computing the coordinates of data in that space.
The kernel trick works by implicitly mapping the input data into a high-dimensional feature space using a kernel function.
A kernel function is a mathematical function that takes in two input vectors and computes a scalar value (dot product) representing the similarity between them.
👉 But why it is called a trick ?
Think of feature engineering: In case of FE, We would “actually” transform the data to higher dimension (lot of computation). But in case of Kernel Trick we are not actually calculating the co-ordinates in higher dimension. We are only calculating the dot product of two vector in higher dimension(Comparatively less computation).
We will evaluate this dot product for every pair of observation. This dot product ( a scaler quantity) acts as a similarity matrix and help SVM compute a decision boundary , or hyperplane, in the high-dimensional feature space, which can then be used to classify new data points.
👉 Lets see this “trickery” with an example : Shall we ?
K(x, y) = . Here K is the kernel function, x, y are n dimensional inputs. f is function map from n-dimension to m-dimension space. denotes the dot product. usually m is much larger than n.
•If x,y are ”similar” , then their dot product would be large.
•If x,y are ” not similar” , then their dot product would be small.
Let, x = (x1, x2, x3); y = (y1, y2, y3).
Let the kernel be K(x, y) = ()^2. [ We are using Polynomial with degree 2]
f(x) = (x1x1, x1x2, x1x3, x2x1, x2x2, x2x3, x3x1, x3x2, x3x3) [Became 9 dimensional , not counting X2X1 same as X1X2 etc]
x = (1, 2, 3); y = (4, 5, 6)
Without kernel trickery:
f(x) = (1, 2, 3, 2, 4, 6, 3, 6, 9) [9 multiplications]
f(y) = (16, 20, 24, 20, 25, 30, 24, 30, 36) [9 multiplications]
= 16 + 40 + 72 + 40 + 100+ 180 + 72 + 180 + 324 = 1024 [9 multiplication + 8 addition]
Total computation = 9 multiplications + 9 multiplications + 9 multiplication + 8 addition = 27 Multiplication + 8 addition
This is needed to compute the dot product ( scaler quantity – 1024 in this example)
With Kernel Trickery:
x = (1, 2, 3); y = (4, 5, 6)
K(x, y) = (4 + 10 + 18 )^2 = 32^2 = 1024
Total computation = 4 multiplications + 3 addition = 4 Multiplication + 3 addition
Same result, with much less computation.
And this my friend is Kernel Trick 🙂
Some commonly used kernel functions include the linear kernel, polynomial kernel, and radial basis function (RBF) kernel. The choice of kernel function depends on the characteristics of the data and the problem at hand.