📚📚 We all know that machine learning algorithms use various distance measures to make sense of data relationships.
🧭 Let’s take a look at few popular distance measure and when these are used :
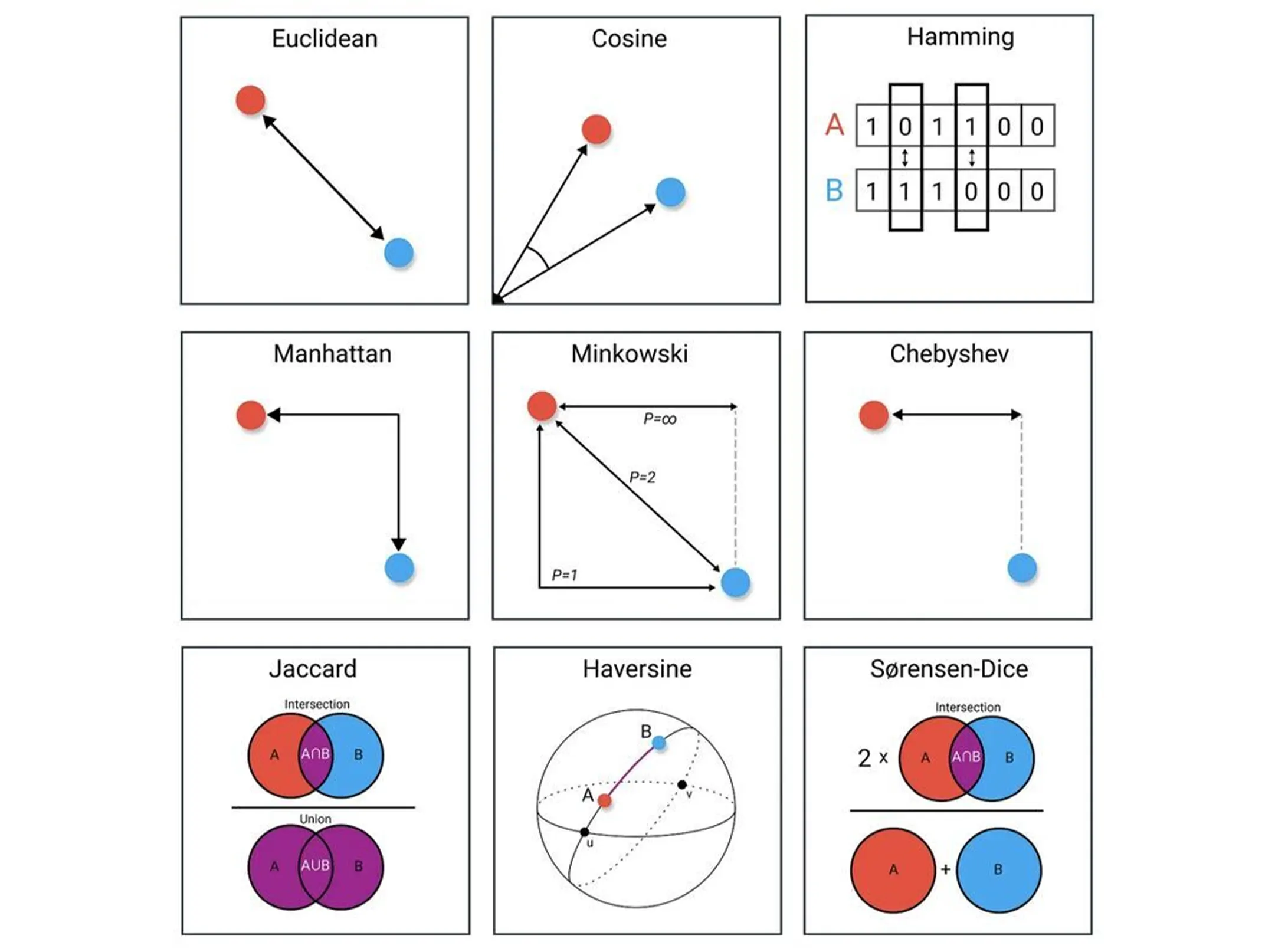
Euclidean Distance: It’s like measuring the “as-the-crow-flies” distance between data points, crucial for clustering and understanding spatial relationships. 🗺️
Cosine Similarity: Think of it as a way to see how aligned the directions of two vectors are, especially helpful for natural language processing and content-based recommendations. 📚
Hamming Distance: This one’s all about counting the differences in binary strings, making it a superhero in error detection, DNA analysis, and more! 🔍
Manhattan Distance: Imagine navigating city blocks; that’s what this L1 distance does! Perfect for robotics and geographic analysis. 🏙️
Minkowski Distance: commonly used in clustering, classification, and recommendation systems. With p as your guide, you can adapt it to fit your specific needs. 🛤️
Chebyshev Distance: It’s like finding the biggest jump between two points, great for spotting outliers and unusual data points. 📈
Jaccard Distance: Set based. It tells you how different two sets are by looking at shared and unique elements. 📑
Haversine Distance: Calculates distances between geographical coordinates, handy for mapping and navigation apps. 🌎
Sørensen-Dice: This one’s into set dynamics, helping us understand shared and distinct elements. Think text analysis and clustering! 📊